HANDBOOK OF INDUSTRIAL MIXING SCIENCE AND PRACTICE

HANDBOOK OF INDUSTRIAL MIXING
SCIENCE AND PRACTICE

This handbook will explain the difference and uses of a variety of mixers including gear mixers, top entry mixers, side entry mixers, bottom entry mixers, on-line mixers, and submerged mixers. It discusses the trade-offs among various mixers, concentrating on which might be considered for a particular process. Handbook of Industrial Mixing explains industrial mixers in a clear concise manner, and gives practical insights by the top professional in the field.

DOWNLOAD

Calibration of blade tip-timing sensor for shrouded blades

Power generation has been of great significance in the production of electric energy for numerous household and industrial use. However, the rapid increase in the demand for electric power has compelled researchers to improve the already existing power generations techniques as well as develop alternative sources to supplement the deficiency. Consequently, the increasing global call for sustainable development as a way of reducing pollution through limiting dependency on fossils fuels have also contributed greatly to such developments. For instance, steam turbines which are highly used in today’s power generation stations have undergone numerous improvements to enhance their efficiency. Unfortunately, it is difficult to realize the smooth operation of turbines, especially for large power generation.
Generally, turbines are made of blades which are susceptible to numerous faults due to the natural frequency, misalignment, unbalancing and vibration. Asynchronous vibrations, for example, are more prevalent, especially for high loaded blades. On the other hand, steam turbine blades commonly undergo synchronous excitation while aerodynamic excitation is caused by resonances with nonsynchronous excitation. To this end, several methods have been devised to prevent unpredictable excitation, dynamic stresses and to improve the lifetime of blades. Blade vibrations have been measured in power stations during wide range operation because mechanical stress damages the blades thus reducing their lifetime. Unfortunately, it is expensive and difficult to use these methods to monitoring more blades due to the short sensor life, especially in corrosive environments. Therefore, researchers have been looking for alternative methods and have identified blade tip timing as a promising solution.
Recently, Zdenek Kubín at the University of West Bohemia in Pilsen in collaboration with Dr. T. Mísek, J. Hlous, T. Dadaková and Dr. J. Kellner at Doosan Škoda Power and Dr. T. Bachorec at SVS FEM investigated the use of eddy current and optical sensors in blade tip timing measurements and calibration in steam power stations. They performed measurements in various conditions and presented the detailed calibration procedure. Eventually, the obtained results were compared to the theoretical ones to validate the feasibility of the model. They purposed to improve the operation efficiency of the steam turbines, reduce damages and improve their lifespan for large power output generation. Their work is published in the journal, Mechanical Systems and Signal Processing.
From the modeled magnetic interference between the blade shroud and sensor, the authors observed that it was capable of predicting the voltage amplitude and shape of signals emanating from the sensors. Consequently, it efficiently identified the axial position responsible for bad signals production. The measurement results correlated well with the existing theoretical results. This included the calibration curve and tip deflection. For instance, best axial positions for the sensors were selected based on the calculated vibration limits and safety factors which were determined based on the measurements and calibration uncertainty. Furthermore, possible causes of such uncertainties included gage position, axial shifts, blade untwists among others.
The authors successfully developed a detailed calibration procedure for blade tip timing sensor that will help advance the efficiency and operation of steam turbines in power generation. It emphasizes on choosing the sensor size and position which was successfully validated by the developed model. The study also provides a groundwork for future studies which will promote power generation to meet the increasing demand for power.

About the author
Zdenek studied Cybernetics and Artificial Intelligence at University of West Bohemia.

source link

Introduction To Shaft types ,Design ,Materials And Applications

Introduction To Shaft types  ,Design ,Materials And Applications

Introduction 
The term shaft usually refers to a component of circular cross-section that rotates and transmits power from a driving device, such as a motor or engine, through a machine. Shafts can carry gears, pulleys, and sprockets to transmit rotary motion and power via mating gears, belts, and chains. Alternatively, a shaft may simply connect to another shaft via a coupling. A shaft can be stationary and support a rotating member, such as the short shafts that support the non driven wheels of automobiles often referred to as spindles.

Types of Shafts
The following two types of shafts are important from the subject point of view :
1. Transmission shafts. These shafts transmit power between the source and the machines absorbing power. The counter shafts, line shafts, over head shafts and all factory shafts are transmission shafts. Since these shafts carry machine parts such as pulleys, gears etc., therefore they are subjected to bending in addition to twisting.
2. Machine shafts. These shafts form an integral part of the machine itself. The crank shaft is
an example of machine shaft
Some common shaft arrangements are shown in Figure 1.

FIG 1

Shaft design considerations
Shaft design considerations include:
1. Size and spacing of components (as on a general assembly drawing), tolerances,
2. Material selection, material treatments,
3. Deflection and rigidity,
         a. Bending deflection,
         b. Torsional deflection,
         c. Slope at bearings,
         d. Shear deflection,
4. Stress and strength,
         a. Static strength,
         b. Fatigue,
         c. Reliability,
5. Frequency response,
6. Manufacturing constraints.
Shafts typically consist of a series of stepped diameters accommodating bearing mounts and providing shoulders for locating devices such as gears, sprockets, and pulleys to butt up against and keys often used to prevent rotation, relative to the shaft, of these “added” components. A typical arrangement for a transmission shaft supporting a gear and pulley wheel illustrating the use of constant diameter sections and shoulders is shown in Figure 2.
Shafts must be designed so that deflections are within acceptable levels. Too much deflection can, for example, degrade gear performance and cause noise and vibration. The maximum allowable deflection of a shaft is usually determined by limitations set on the critical speed, minimum deflections required for gear operation, and bearing requirements. In general, deflections should not cause mating gear teeth to separate more than about 0.13 mm and the slope of the gear axes should not exceed about 0.03 . The deflection of the journal section of a shaft across a plain bearing should be small in comparison with the oil film thickness. Torsional and lateral deflection both contribute to lower critical speed.

FIG 2

shaft angular deflection at rolling element bearings should not exceed 0.04⁰, with the exception being self-aligning rolling element bearings. Shafts can be subjected to a variety of combinations of axial, bending, and torsional loads (see Figure .3) which may fluctuate or vary with time. Typically, a rotating shaft transmitting power is subjected to a constant torque together with a completely reversed bending load, producing a mean torsional stress and an alternating bending stress respectively.

FIG 3

Shafts should be designed to avoid operation at, or near, critical speeds. This is usually achieved by the provision of sufficient lateral rigidity so that the lowest critical speed is significantly above the range of operation. If torsional fluctuations are present (e.g. engine crankshafts, cam-shafts, compressors) the torsional natural frequencies of the shaft must be significantly different to the torsional input frequency. This can be achieved by providing sufficient torsional stiffness so that the shaft’s lowest natural frequency is much higher than the highest torsional input frequency.
Rotating shafts must generally be supported by bearings. For simplicity of manufacture, it is desirable to use just two sets of bearings. If more bearings are required, precise alignment of the bearings is necessary. Provision for thrust load capability and axial location of the shaft is normally supplied by just one thrust bearing taking thrust in each direction. It is important that the structural members supporting the shaft bearings are sufficiently strong and rigid.
The following list outlines a shaft design procedure for a shaft experiencing constant loading. The flow charts given in (Figures 4) can be used to guide and facilitate design for shaft strength and rigidity and fluctuating load capability. 

FIG 4

1. Determine the shaft rotational speed.
2. Determine the power or torque to be transmitted by the shaft.
3. Determine the dimensions of the power transmitting devices and other components mounted on the shaft and specify locations for each device.
4. Specify the locations of the bearings to support the shaft.
5. Propose a general form or scheme for the shaft geometry considering how each component will be located axially and how power transmission will take place.
6. Determine the magnitude of the torques throughout the shaft.
7. Determine the forces exerted on the shaft.
8. Produce shearing force and bending moment diagrams so that the distribution of bending
moments in the shaft can be determined.
9. Select a material for the shaft and specify any heat treatments, etc.
10. Determine an appropriate design stress taking into account the type of loading (whether
smooth, shock, repeated, reversed).
11. Analyze all the critical points on the shaft and determine the minimum acceptable diameter at each point to ensure safe design.
12. Determine the deflections of the shaft at critical locations and estimate the critical frequencies.
13. Specify the final dimensions of the shaft. This is best achieved using a detailed manufacturing drawing to a recognized standard and the drawing should include all the information required to ensure the desired quality. Typically, this will include material specifications, dimensions, and tolerances (bilateral, runout, data, etc.)surface finishes, material treatments, and inspection procedures.


Basic Equations
free-body diagram (Figure 5)

FIG 5

The various equations required to evaluate the stresses and strains in a loaded shaft and to arrive at safe operating loads are to be found in books or web . The simple equations below related to the estimating the torque resulting from a transmitted power and the surface shear stresses resulting from a transmitted torque.

where :

T : shaft torque (Nm)

𝜔 : angular velocity (Rads/sec)

n : RPM (revs /min)
P = Power transmitted (kW)

where :

σ = Direct stress (N/m²)

τ = Shear stress (N/m²)

M = Applied bending moment (N.m)

D = Shaft diameter(m)

I = Moment of Inertia (m⁴ - more normally cm⁴)

 This is very relevant to ductile metals. It is conservative and relatively easy to apply. It assumes that failure occurs when a maximum shear stress attains a certain value. This value being the value of shear strength at failure in the tensile test. In this instance it is appropriate to choose the yield point as practical failure. If the yield point = Sy and this is obtained from a tensile test and thus is the sole principal stress then the maximum shear stress Ssy is easily identified as Sy /2 .

Ssy = Sy /2

where :

Ssy = Shear yield strength (N/m²)
Sy = Tensile yield strength (N/m²)

Maximum Shear Stress = τ max = Greatest of ( σ1 - σ2 ) / 2 : ( σ2 - σ3 ) / 2 : ( σ1 - σ3 ) / 2 = ( σ1 - σ3 ) / 2

The factor of safety selected would be

FoS = Sy / ( 2 . τ max ) = Sy / ( σ1 - σ3 )

For the simple case of a tensile stress σx combined with a shear stress τ xy . with the principal stress σ3 = 0. and σy ,σz τxz , τzy = 0. .. (ref to notes on Mohrs circle) .. Mohr's Circle The two non-zero principal stresses are :

where :

σ1 ,2, 3 = Principal Stresses(N/m²)

σx ,y, z = Direct stress z ,y and z directions(N/m²)

τxy = Shear stress in xy plane (N/m²)

The resulting FoS = 

Or in terms of Torque and bending moments.

For a typical application of a shaft subject to direct stress, torque, and a bending moment the mohrs circle is as follows

where:

D = Shaft diameter(m)

Km = Shock fatigue factor. ( Moments )

Kt = Shock / fatigue factor. (Torques.)

For a rotating shaft there is a speed at which, for any small initial deflection, the centripetral force is equal to the elastic restoring force. At this point the deflection increases greatly and the shaft is said to "whirl". Below and above this speed this effect is very much reduced. This critical (whirling speed) is dependent on the shaft dimensions, the shaft material and the shaft loads . The critical speed is the same as the frequency of traverse vibrations.

The critical speed Nc  of a shaft is simply

Where

 m = the mass of the shaft assumed concentrated at single point .
k  =the stiffness of the shaft to traverse vibrations

For a horizontal shaft this can be expressed as

Where

y = the static deflection at the location of the concentrated mass

g = acceleration due to gravity (m.s-² )
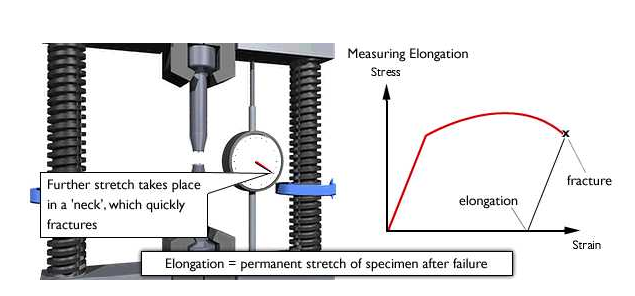
Shaft Deflection

Maximum deflection is an important parameter when considering functionality of the shaft. Its maximum permitted value depends on the type of shaft, its function and structural features. The following recommendations can be applied for its size (shaft with toothed wheel):

At the point of seating of the toothed wheel
for spur gearing y = 0.01 * m
for bevel and worm wheels y = 0.005 * m
[m...module of toothed wheel]

Or recommended maximum deflection (not at points of seating of wheels) is for:
General engineering y = 0.0003 * L
Construction of machine tools y = 0.0002 * L
[L...distance between bearings]
The angular deflection of the shaft at points of seating of the toothed wheel should not exceed a value between 0.05° and 0.12° (3' - 7').
The angular deflection at bearing points depends on the type and inner structure of the bearing. Generally applicable:

forces on shafts examples

Indicative Transmittable Torque Values
This table is provided to allow comparison between shafts and is based on very simplistic assumptions with no allowance for fatigue, additional stresses to Bending Moments

Shaft materials And Applications 

The choice of steel for a particular application can sometimes be a bewildering experience. Within the current British Standard alone for steels (BS970), there are several hundred steel specifications. In practice, relatively few steels are used for the majority of applications, and some of the popular specifications are listed below.

Steels can be divided into seven principal groupings.

1. Low carbon free cutting steels. These are the most popular types of steel for the production of turned components, where machinability and surface finish are important. Applications include automotive and general engineering. The principal specification is 230M07.

2. Low carbon steels or mild steels. These are used for lightly stressed components, welding, bending, forming, and general engineering applications. Some of the popular specifications are 040A10, 045M10, 070M20, 080A15, and 080M15.

3. Carbon and carbon manganese case hardening steels. These steels are suitable for components that require a wear resisting surface and tough core. Specifications include 045A10, 045M10, 080M15, 210M15, and 214M15.

4. Medium carbon and carbon manganese steels. These offer greater strength than mild steels and respond to heat treatment. Tensile strengths in the range of 700e1000 MPa can be attained. Applications include gears, racks, pinions, shafts, rollers, bolts, and nuts. Specifications include 080M30, 080M40, 080A42, 080M50, 070M55, and 150M36.

5. Alloy case-hardening steels. These are used when a hard wear resisting surface is required but, because of the alloying elements, superior mechanical properties can be attained in comparison with carbon and carbon manganese case-hardening steels. Typical applications include gears, cams, rolled, and transmission components. Types include 635M15,

655M13, 665M17, 805M20, and 832M13.

6. Alloy direct hardening steels. These steels include alloying elements such as Ni, Cr, Mo, and Vand are used for applications where high strength and shock resistance are important. Types include 605M36, 708M40, 709M40, 817M40, and 826M40.

7. Stainless steels. There are three types of stainless steels: martensitic, ferritic, and austenitic.

Martensitic stainless steels can be hardened and tempered to give tensile strengths in the range from 550 to 1000 MN/m2. Applications include fasteners, valves, shafts, spindles, cutlery, and surgical instruments. Specifications include 410S21, 420S29, 420S45, 431S29, 416S21, 416S41, 416S37, and 441S49.

Ferritic stainless steels are common in strip and sheet form, and applications include domestic and automotive trim, catering equipment, and exhaust systems. They have good ductility and are easily formed. Specifications include 403S17 and 430S17. Austenitic stainless steels offer the highest resistance to corrosion, and applications are affiliated with the food, chemical, gas, and oil industries, as well as medical equipment and domestic appliances. Specifications include 302S31, 304S15, 316S11, 316S31, 320S31, 321S31, 303S31, 325S31, 303S42, and 326S36.

  some steel types and typical material property values.

Engineering Materials 1 An Introduction to their Properties and Applications Second Edition by Michael F. Ashby and David R. H. Jones

Engineering Materials 1
An Introduction to their Properties and Applications
Second Edition
by
Michael F. Ashby
and
David R. H. Jones

This book gives a broad introduction to these properties and limitations. It cannot make you a materials expert, but it can teach you how to make a sensible choice of material, how to avoid the mistakes that have led to embarrassment or tragedy in the past, and where to turn for further, more detailed, help.

DOWNLOAD

ADVANCES IN THE TECHNOLOGY OF STAINLESS STEELS AND RELATED ALLOYS ASTM Special Technical Publication No. 369

ADVANCES IN THE TECHNOLOGY
OF STAINLESS STEELS AND
RELATED ALLOYS
ASTM Special Technical Publication No. 369

During 1963 the American Society for Testing and Materials; the Metallurgical Society of the American Institute of Mining, Metallurgical, and Petroleum Engineers; and The Electrochemical Society and the National Association of Corrosion Engineers, organized symposia dealing with several aspects of the technology of stainless steels.
Members of these organizations who were concerned with these activities decided that it would be advantageous to those interested in stainless steels if the papers presented at these meetings could be combined in a single pubhcation for convenient future reference.
They formed an Intersociety Co-ordinating Committee to accomphsh this. With the collaboration of the authors of the several papers, the participating societies, and particularly the American Societ\- for Testing and Materials which undertook publication of the papers in this volume, the desired consolidation of papers from the several societies has been achieved.
The symposia in which the several papers originated were as follows: (1) symposium on Advances in the Technology of Stainless Steels and Related Alloys, Atlantic City, N. J.,
June, 1963, Sponsored by ASTM Committee A-10, M. A. Cordovi, chairman; (2) symposiumon Stress Corrosion Cracking, H. L. Logan, E. H. Phelps, and H. R. Copson, co-chairmen, and symposium on Evaluation Tests for Stainless Steels, R. B. Mears,
chairman. Second International Congress on Metallic Corrosion Sponsored by NACE in collaboration with The Electrochemical Soc, New York, N. Y., March, 1963; and (3) symposium on Recent Advances in the Metallurgy of Stainless Steels, Cleveland, Ohio, October, 1963, sponsored by the Metallurgical Society of AIME, E. J. Dulis and L. R. Scharfstein, co-chairmen.
The task force concerned with this activity wishes to express its thanks to all who have co-operated in this venture. It is hoped that the results of this effort will be well received by those in whose interests it was undertaken and that its success will prompt similar future action in consoHdating information from several sources in single publications
for more convenient reference.

download

STABILITY AND DUCTILITY OF STEEL STRUCTURES Edited by Professor Dan DUBINA Professor Mikl6s IVANYI

STABILITY AND DUCTILITY OF
STEEL STRUCTURES
Edited by
Professor Dan DUBINA
Professor Mikl6s IVANYI

With the gradual development of rules for designing against instability the idea emerged, in London, in 1974 to hold an International Colloquium treating every aspect of structural instability of steel structures.

There have been 17 International Colloquia Stability Sessions around the world, starting with the first one in Paris in 1972, until with the last one in Nagoya in 1997. In Nagoya it was decided to continue the series of travelling colloquia by launching the Sixth Colloquium in September 1999 with the First Session to be held at the "Politehnica" University of Timişoara, România, which will be followed by another in the year 2000 at the Gediminas Technical University in Vilnius, Lithuania, a third one during SSRC's Year 2000 Annual Meeting in the US, and a fourth one in Australia or New Zealand.

At present important research projects are in progress around the world, like SAC Joint Venture Project in USA, INCO-COPERNICUS "RECOS" in Europe and others, which are devoted to improve and develop new methods for the safety design of steel structures in seismic zones. Special attention is paid in Europe, USA and Japan to improve the design codes and detailing of seismic resistant steel structures.

This was the reason to organise the Session of Nagoya as "Stability and Ductility of Steel Structures" Colloquium. Romania is also a strong seismic territory and therefore, the topic of the Timişoara Session covered both stability and ductility problems. The technical programme of the SDSS'99 Colloquium in Timişoara has been split into nine working sessions.

DOWNLOAD

ABUDEN ToolBox Version 2015 R2

ABUDEN ToolBox 

Version 2015 R2

The ABUDEN toolbox is designed for technical inspectors with the following features.

Design and implementation of ASME SEC II smart tables
Design and implementation of ASME B31.1 smart tables
Design and implementation of ASME B31.3 smart tables
Design and implementation of ASME B16.01 smart tables
Design and implementation of ASME B16.05 smart tables
Design and implementation of ASME B16.09 smart tables
Design and implementation of ASME B16.11 smart tables
Design and implementation of ASME B16.21 smart tables
Design and implementation of ASME B16.47 smart tables
Design and implementation of ASME B36.10 smart tables
Design and implementation of ASME B36.19 smart tables
Design and implementation of AISC dimensional information
Design and implementation of ASME IX P NUMBER smart tables
Design and implementation of ASME IX F NUMBER smart tables
Design and implementation of ASME IX A NUMBER smart tables
Design and implementation of ASME IX APP.D smart tables
Perform MRT calculations for CYLINDER based on ASME SEC VIII Div.1
Perform MRT calculations for SPHERICAL based on ASME SEC VIII Div.1 compression
Performing MRT calculations for CONICAL based on the ASME SEC VIII Div.1 press release
Performing MRT calculations for ELLIPTICAL based on ASME SEC VIII Div.1
Perform MRT calculations for TORISPHERICAL based on ASME SEC VIII Div.1
Performing MRT calculations for TORICONICAL based on the ASME SEC VIII Div.1 Compactor
Performing MRT Calculations for CYLINDER Based on ASME SEC VIII Div.2
Performing MRT Calculations for SPHERICAL Based on the ASME SEC VIII Div.2
Conducting MRT calculations for CONICAL based on ASME SEC VIII Div.2.
Performing MRT Calculations for ELLIPSOIDAL Based on ASME SEC VIII Div.2
Performing MRT calculations for TORISPHERICAL on the basis of an ASME SEC VIII div.2
Performing Level 1 calculations based on API 579-2007 compression
Performing the standard calculations of AS

•                                                             
• DOWNLOAD

Handbook of Aluminum Volume 1 Physical Metallurgy and Processes

Handbook
of Aluminum
Volume 1
Physical Metallurgy and Processes


The Handbook of Aluminum: Vol. 1: Physical Metallurgy and Processes covers all aspects of the physical metallurgy, analytical techniques, and processing of aluminium, including hardening, annealing, aging, property prediction, corrosion, residual stress and distortion, welding, casting, forging, molten metal processing, machining, rolling, and extrusion. It also features an extensive, chapter-length consideration of quenching.

DOWNLOAD

METALLIC MATERIALS Physical, Mechanical, and Corrosion Properties Philip A. Schweitzer, P. E.

METALLIC
MATERIALS
Physical, Mechanical, and
Corrosion Properties
Philip A. Schweitzer, P. E.



Metallic Materials compares and contrasts the corrosion resistance of wrought stainless steel and high nickel alloys and explores recent advances in the production of exotic metals. It emphasizes the physical and mechanical properties, corrosion resistance, workability and cost of various metals. The authors analyze the physical and mechanical properties of metals, define relevant terminology, describe the various forms of corrosion to which metals may be susceptible, examine wrought ferrous metals, alloys, and typical applications, and cover wrought nickel and high nickel alloys. This is a handy reference for the busy engineer and student in corrosion, materials, chemical, mechanical, civil, design, process, metallurgical, manufacturing, and industrial engineering.

download

STP 1256 Fracture Mechanics: 26th Volume Walter G. Reuter, John H. Underwood, and James C. Newman, Jr., Editors

STP 1256
Fracture Mechanics:
26th Volume
Walter G. Reuter, John H. Underwood, and
James C. Newman, Jr., Editors


The ASTM National Symposium on Fracture Mechanics is sponsored by ASTM Committee E08 on Fatigue and Fracture Testing. The original objective of these symposia was to promote technical interchange between researchers from the United States and worldwide in the field of Fracture. This objective was recently expanded to promote technical interchange between researchers in the field of fatigue and fracture. The meeting attracted about 100 researchers covering a broad range of issues in constraint, weldments, advanced materials, and practical applications.
The volume opens with the paper by Merkle who delivered the Fifth Annual Jerry L. Swedlow Memorial Lecture at this symposium. Merkle's presentation provided a brief philosophical and historical overview of applied fracture mechanics, particularly as it pertains to the safety of pressure vessels. The importance of constraint, a fundamental aspect of fracture mechanics in which Jerry Swedlow had a keen interest and made valuable contributions, was presented along with the need for physically realistic analysis. Additional insight into constraint effects on fracture toughness was developed by considering the roles played by the plastic strains, as well as the stresses that develop near a crack tip.
There are 42 papers following the Merkle paper that are broadly grouped in the same categories used to separate the presentation at the symposium. The constraint issue was separated into Crack Initiation with seven papers examining J or CTOD, and Crack Growth with seven papers investigating plane strain or plane stress conditions. Following these papers, there is a section on Weldment with eight papers. These papers are primarily concerned with effects of weld metal mismatch on the fracture process. The remaining papers discuss strain aging and nodular cast iron. The next section on Engineered Materials contains nine papers that cover a variety of topics consisting of monotonic or cyclic loading of ceramics, composites, adhesive joints, graded materials, paper, and an A1-Li alloy. The last three sections consist of Subcritical Crack Growth with five papers that present results of studies on fatigue, creep, or stress corrosion crack growth; Dynamic Loading with two papers; and Applications with four papers.
The technical quality of these papers is due to the authors and to the fine reviews provided by the reviewers. The symposium organizers would like to express our appreciation to all reviewers for a job well done. Because of the large number of papers, camera-ready manuscripts were used to develop the STP. The organizers of the symposium hope that it meets your approval.
The National Symposium on Fracture Mechanics is often used to present ASTM awards to recognize the achievement of current researchers. At the Twenty-Sixth Symposium, the award for the Jerry L. Swedlow Memorial Lecture was presented to Dr. John G. Merkle,
Oak Ridge National Laboratory. The Award of Merit was presented to Professor Ashok Saxena, Georgia Institute of Technology. Awards of Appreciation were presented to Dr. Mark T. Kirk, Dr. James C. Newman, Jr., and to Professor Ad Bakker, Delft University of Technology. The organizing committee would like to congratulate the above award winners as considerable time, effort, and hard work were required to win these awards.

download

An Introduction To Mechanical properties Of Material

An Introduction To Mechanical properties Of Material 


Introduction 
The  describe the physical properties of a material, this means  how it is likely to behave whilst it is being processed and when it is in service.  such as strength, hardness, toughness and corrosion resistance. These now need to be carefully defined so that wherever possible, they can be measured.
Physical properties can be sub-divided into mechanical properties, thermal properties, electrical and magnetic properties and durability.now we.ll explain mechanical properties

Mechanical Properties
These include density, tensile strength, hardness, toughness, ductility, malleability, elasticity and brittleness...etc  (Figure 1) .They are defined as follows.

FIG 1

Density
Density is the mass in kilograms, contained in a cubic meter of a material or substance. When used in calculations, it is usually denoted by the Greek letter 𝜌 (rho) and its units are kilograms per cubic meter (kg.m³).

FIG  2

The density of steel is around 7800 kgm³ and that of cast iron is around 7300 kgm³. The densities of the major non-ferrous metals used in engineering are listed in Table 1.
When designing aircraft, engineers need to be able to estimate the weight of the different components and then the total weight. Knowing the densities of the different materials helps them do this.

TABLE 1

Specific Gravity
Specific gravity is the ratio of the density of the metal to the density of a reference material, usually water at a specified temperature and pressure. Specific gravity is unitless.
Tensile strength
The tensile strength of a material is a measure of its ability to withstand tensile forces. The Ultimate Tensile Strength (UTS) is the tensile stress that causes a material to fracture. If you have completed the unit Science for Technicians, you will know that tensile stress is the load carried per square meter of cross-sectional area. Its units are thus Newtons per square meter or Pascals (Pa)

FIG 3

The UTS of mild steel is around 500 MPa. The values of UTS for other ferrous and non-ferrous metals are given in Tables 2,3, and 4. Sometimes material suppliers quote the UTS of a
material in Newtons per square millimeter (N mm²). It is useful to know that the value is numerically the same in both mega pascals and Newtons per square millimeter, i.e. the UTS of mild steel
can be written as 500 MPa or 500 N mm².

TABLE 2

TABLE 3

TABLE 4

The Ultimate Tensile Strength of a material can be determined by carrying out a destructive tensile test on a prepared specimen (Figure 3). The specimen is gripped in the chucks of a tensile
testing machine and increasing values of tensile load are applied up to the point of fracture. Depending on the type of machine, the load is applied by means of hydraulic rams, a lever system or a lead screw. Its value is read off from an analogue or a digital display.
The extension of the specimen can be measured by means of an extensometer that is attached to the specimen. This can be of the Lindley type, which records the extension on a dial test indicator,
or the Monsanto type, which operates on the micrometer principle.
There is also an electrical type, which is a linear variable differential transformer. This can be interfaced with an x–y plotter or a computer to produce a graph of load v. extension (FIG 4)

FIG 4

The extension of a specimen is usually measured over a gauge length of 50 mm. The initial diameter is checked using a micrometer and the initial cross-sectional area A, is calculated. The UTS of the material can then be calculated using the formula :

Ductility
The ductility of a material is a measure of the amount by which it can be drawn out in tension before it fractures. As can be seen from the typical load v. extension graphs in Figure 4., copper has a high degree of ductility and this enables it to be drawn out into long lengths of wire and tube. There are a number of different
ways in which ductility can be measured. One method is to carry out a bend test in which a sample of material is bent through an angle and observed for the appearance of cracks. The angle at  which cracking or breaking occurs gives a measure of ductility.
Ductility measurement can also be incorporated in a tensile test. Before a tensile test, the gauge length over which extension is measured is centre punched. After the test, the two pieces of the
fractured specimen are placed in contact and the elongation of the gauge length is measured. The ductility can then be calculated as the percentage increase in the gauge length.

Alternatively, the diameter at the point of fracture can be measured and the cross-sectional area calculated. The ductility can then be calculated as the percentage reduction in area.

When a ductile material fails, the appearance of the fracture is as shown in Figure 5

FIG 5

As the maximum load is approached, a neck or waist is seen to form at the point where fracture will occur. When the fracture surfaces are examined it is found that they have a characteristic cup and cone appearance which is typical of ductile materials.
When ductile materials are loaded, a point is reached known as the elastic limit. If this is exceeded, elastic failure is said to have occurred. This is followed by plastic deformation up to the point
of fracture. If a material is unloaded within the plastic extension range, it does not return to its original shape and there is permanent deformation (Figure 6).

FIG 6

Mild steel has the characteristic load v. extension graph shown in Figure 4. Its elastic limit is followed closely by the yield point where the material suddenly gives way under the load. Elastic
failure is then said to have occurred. If the material is loaded beyond this point there will be some permanent deformation when the load is removed.
Mild steel behaves in this way because of the interstitial carbon atoms. They are said to ‘pin’ the planes of iron atoms within the grains, which stops them from slipping under load. Eventually
they can no longer hold the iron atoms and yielding takes place.
For a short time, extension occurs at a reduced load but the material soon becomes work hardened and the load v. extension graph then rises in a curve until the maximum load is reached. It is
important to know the stress at which yielding takes place in steel components so that they can be designed to operate below the yield point load.

Compressive strength
This is the ability of a material to withstand compressive (squeezing) loads without being crushed or broken. The material is in compression
Brittleness
This is the opposite of ductility. When metals are loaded in tension they first undergo elastic deformation which is proportional to the load applied. When unloaded from within the elastic range, the material returns to its original shape. 
Brittle materials tend to fail within the elastic range, or very early in the plastic range, before
very much deformation has taken place. Cast iron is brittle, as can be seen from its load v. extension graph in Figure 4. Brittle materials very often fracture across a plane at right angles to the direction of loading. Sometimes however, the fracture plane is at 45⁰ to the direction of loading as shown in Figure 7. This indicates that the material has a low shear strength.

FIG 7

Toughness: impact resistance
This is the ability of a material to resist shatter. If a material shatters it is brittle (e.g. glass). If it fails to shatter when subjected to an impact load it is tough (e.g. rubber). Toughness should not be confused with strength. Any material in which the spread of surface cracks does not occur or only occurs to a limited extent is said to be tough.

FIG 8

Elasticity
This is the ability of a material to deform under load and return to its original size and shape when the load is removed. Such a material would be required to make the spring as shown.

FIG 9 

If you have completed the unit Science for Technicians you will know that the modulus of elasticity of a material is given by the formula

Plasticity
This property is the exact opposite of elasticity. It is the state of a material which has been loaded beyond its elastic state. Under a load beyond that required to cause elastic deformation (the elastic limit) a material possessing the property of plasticity deforms permanently. It takes a permanent set and will not recover when the load is removed.

FIG 10

Malleability
Whereas ductility is the ability of a material to be drawn out in tension, malleability is the ability of a material to be deformed or spread in different directions. This is usually caused by compressive
forces during rolling, pressing and hammering operations.
Copper is both ductile and malleable but the two properties do not necessarily go together. Lead is extremely malleable but not very ductile, and soon fractures when loaded in tension.
A malleable material combines the properties of plasticity and compressibility, so that it can be squeezed to shape by such processes as forging, rolling and rivet heading.

FIG 11

Hardness
This is the ability of a material to withstand scratching (abrasion) or indentation by another hard body. It is an indication of the wear resistance of a material.

FIG 12

Processes which increase the hardness of materials also increase their tensile strength. At the same time the toughness of the material is reduced as it becomes more brittle.
Hardenability must not be confused with hardness. Hardenability is the ability of a metal to respond to the heat treatment process of quench hardening. To harden it, the hot metal must be chilled at a rate in excess of its critical cooling rate. Since any material cools more quickly at the surface than at the center there is a limit to the size of bar which can cool quickly enough at its center to achieve uniform hardness throughout. This is the ruling section for the material. The greater its hardenability the greater will be its ruling section.

FIG 13

The hardness test is the most utilized mechanical property test of all methods available. These tests do not require much time and are very informative since hardness is related to strength. See Table 5.

TABLE 5

Shear strength
This is the ability of a material to withstand offset or transverse loads without rupture occurring. The rivet connecting the two bars shown is in shear whilst the bars themselves are in tension. Note that the rivet would still be in shear if the bars were in compression.

FIG 14

Elongation
Elongation is a measure of ductility, as measured by the percentage of elongation. Increasing the gauge length of a specimen will decrease the percent of elongation to fracture. This is because after the neck forms all subsequent deformation takes place in the vicinity of the neck. The behavior around the neck is the same regardless of the length of the specimen. Therefore in shorter gauge lengths, a larger fraction of the specimen’s length is deforming during the test. In longer specimens, the portion away from the neck is not continuing to deform after the onset of necking, therefore a smaller percentage of the specimen’s length is contributing to the total deformation.
Because of this it is necessary to compare percents of elongation of various metals with the same gauge length when comparing ductility.

FIG 15

Creep
Creep is a time-dependent deformation of a material while under an applied load that is below its yield strength. It is most often occurs at elevated temperature, but some materials creep at room temperature. Creep terminates in rupture if steps are not taken to bring to a halt.

Creep data for general design use are usually obtained under conditions of constant uniaxial loading and constant temperature. Results of tests are usually plotted as strain versus time up to rupture. As indicated in the image, creep often takes place in three stages. In the initial stage, strain occurs at a relatively rapid rate but the rate gradually decreases until it becomes approximately constant during the second stage. This constant creep rate is called the minimum creep rate or steady-state creep rate since it is the slowest creep rate during the test. In the third stage, the strain rate increases until failure occurs.

FIG 16

Creep in service is usually affected by changing conditions of loading and temperature and the number of possible stress-temperature-time combinations is infinite. While most materials are subject to creep, the creep mechanisms is often different between metals, plastics, rubber, concrete.

Stiffness

It is defined as the property of a material which is rigid and difficult to bend. The example of stiffness is rubber band. If single rubber band is stretch by two fingers the stiffness is less and the flexibility is more. Similarly, if we use the set of rubber band and stretched it by two fingers, the stiffness will be more, rigid and flexibility is less.

The expression of stiffness for an elastic body is as below.

Here, the stiffness is k, applied force is F, and deflection is δ.
The unit of stiffness is Newtons per meter.

resilience

resilience is the ability of a material to absorb energy when it is deformed elastically, and release that energy upon unloading. Proof resilience is defined as the maximum energy that can be absorbed up to the elastic limit, without creating a permanent distortion. The modulus of resilience is defined as the maximum energy that can be absorbed per unit volume without creating a permanent distortion. It can be calculated by integrating the stress–strain curve from zero to the elastic limit. In uniaxial tension, under the assumptions of linear elasticity,

The area under the linear portion of a stress–strain curve is the resilience of the material (figure 17)

FIG 17

where
Ur is the modulus of resilience,
σy is the yield strength,
εy is the yield strain,
and E is the Young's modulus This analysis is not valid for non-linear elastic materials like rubber, for which the approach of area under the curve till elastic limit must be used.

fatigue

fatigue is the progressive and localised structural damage that occurs when a material is subjected to cyclic loading. The maximum stress values are less than the ultimate tensile stress limit, and may be below the yield stress limit of the material. 

FIG 18