AXIAL AND CENTRIFUGAL FANS
AXIAL AND CENTRIFUGAL FANS
introduction
Any device which produces a current of air may be called a fan. This discussion will be limited to fans which have a rotating impeller to produce the flow and a stationary casing to guide the flow into and out of the impeller. The form of the casing or the impeller may vary widely.
Fan Classification
One of the characteristics by which fans are classified is the nature of the flow through the blade passages of the impeller. Axial flow, radial flow, mixed flow, and cross flow are all possible in fan impellers. Certain fan names result from these classifications. Other fan names derive from other characteristics.
1-Propeller fans, tube-axial fans, and vane-axial fans all utilize axial flow impellers, but their casings differ. Propeller fans may be mounted in a ring or panel. Tube-axial fans and vane-axial fans both use tubular casings, but for vane-axial fans they are equipped with stationary guide vanes.
A great deal of the energy transferred to the air in axial-flow machines is in kinetic form. Some of this kinetic energy can be transformed
into pressure energy by straightening the swirl, e.g., with vanes, or by reducing the exit velocity, e.g., with a diffuser. Propeller fans effect very little transformation and hence have very low pressure-producing capability. Vane-axial fans can be equipped for maximum transformation as well as high transfer of energy and hence have high pressure- producing potential depending on tip speed and blade angles. High hub ratios promote high energy transfer.
2- Centrifugal fans and tubular centrifugal fans both utilize radial-flow impellers. Centrifugal fans usually employ a volute or scroll-type casing, the flow entering the casing axially and leaving tangentially. Tubular centrifugals use tubular casings so that the flow both entering and leaving
the casing is axial. A considerable portion of the energy transferred to the air in a radial-flow machine is due to centrifugal action; hence the name centrifugal fan. Since centrifugal action varies with blade depth, the pressure-producing capability of radial-flow fans will vary with this
factor as well as tip speed and blade angles.
Mixed-flow impellers can be used in either axial or scroll-type casings. They are characterized as mixed flow because both axial and radial flow take place in the blading. Mixed-flow impellers used in axial-flow casings have a hub similar to a pure axial-flow impeller, but the inlet portion of the blading extends down over the face of the hub, thereby giving some radial guidance. Mixed-flow impellers used in scroll-cased fans have blades which give most of the axial guidance in the inlet
portion and most of the radial guidance in the discharge portion.
In a cross-flow impeller, the air passes through the blading twice, entering more or less tangentially through the tip, passing across the impeller and out the other side. The casings are designed to provide this transverse flow. Cross-flow fans are also known as tangential fans or transverse-flow fans. Pressure-producing potential is low and depends on the formation of a vortex as the air leaves the impeller
Ring-shaped in which the circulation of air or gas in a toric casing is helicoidal. The rotation of the impeller, which contains a number of blades, crates a helicoidal trajectory which is intercepted by one or more blade, depending on the flowrate. The impeller transfers energy to the air
or gas and is usually used for very low flowrates
Apart from the effects of varying blade widths and inlet areas, other differences in fan characteristics are attributable to differences in blade shape.
1-Forward curved blades
These impellers first became popular at the end of the 19th Century and almost superseded all other types. A diagrammatic representation of the impeller is shown in Figure They are considerably smaller for a given duty than all other designs.
 |
| fig1 |
2-Deep vane forward curved blades
These blades are considerably stronger than the conventional forward curved, being triangulated. They can thus run at higher speeds developing high pressure.
3- Shrouded radial blades
This useful design is represented diagrammatically in Figure and can handle free flowing dust-laden air or gas. The impellers have the ability to deal with higher burdens than the backward inclined type. They are somewhat more efficient (up to 65% static) than the open paddle and also able to run at higher rotational speeds and thus develop higher pressures.
The blades are inherently strong, as centrifugal forces have no bending effect. They are also simple and in sizes up to 900 mm can be easily flanged for rivetting and spot welding.
Blades are largely self-cleaning and are easily cleaned. Such fans are suitable for moderate free-flowing granular dust burdens.
4-Open paddle blades
This is the impeller for heavy dust burdens in excess of those possible with the shrouded radial. Its efficiency is only moderate (up to 60% static) but it is suitable for high temperatures. As
there are no shrouds or backplates, the blades are free to expand. Standard units may therefore be used with gases up to 350° but special alloy wheels can be designed for the very highest temperatures.
5- Backplated paddle impellers
Where the solids are fibrous in character, e.g. wool, paper, or wood shavings, there is tendency for them to wrap round the shaft of an open paddle and clog the unit. The backplate obviates
this possibility. All characteristics are generally as the open paddle, except that the backplate paddle need to run about 3% faster taking approximately 6% more power for duties in its optimum range.
6- Radial tipped blades
This blade form is used as an alternative to the shrouded radial. Generally there is an increased number of blades and the heel of these is forward curved to reduce shock losses. The efficiency
and flowrate are therefore improved for a given size, but the characteristics are otherwise similar. Fan static efficiencies up to 73% are possible
7- Backward inclined blades
These may be considered at the "maids of all work". Due to their simplicity the blades lend themselves to simple methods of construction, at a moderate price, and they can easily be flanged for rivetting and spot welding up to size 900 mm. The design is of the high-speed type making them suitable for direct connection (Arrangement 4 and 8 for many duties).
8- Backward curved blades
These impellers are shown in Figure and are preferred for certain applications where there may be disadvantages in the use of the backward inclined type. Due to the curvature, the blade angle at inlet can be made steeper for a given outlet angle. This generally enables shock losses to be kept low, whilst the curvature itself develops a certain degree of lift. It is therefore possible to arrange such fans with a pressure curve continually rising to zero flow.
9- Reverse curve blades
These blades are backward curved at their tips but forward curved at the heel. Characteristics are generally similar to the backward curved type with the same limitations to their use. Shock losses at entry to the blade passages is reduced however and a slightly higher efficiency maintained outside the range of the b.e.p.
10- Backward aerofoil blades
The impeller is shown in Figure. The blades produce lift forces, which counteract inter-blade circulation without requiring precise angles. Thus smooth flow conditions are maintained
over a considerable portion of the characteristic
Fan Selection Criteria
Before selecting a fan, the following information is needed.
• Air volume required - CFM
• System resistance - SP
• Air density (Altitude and Temperature)
• Type of service
• Environment type
• Materials/vapors to be exhausted
• Operation temperature
• Space limitations
• Fan type
• Drive type (Direct or Belt)
• Noise criteria
• Number of fans
• Discharge
• Rotation
• Motor position
• Expected fan life in years
FAN PERFORMANCE AND TESTING
Subscripts
1 =fan inlet plane
2= fan outlet plane
a =absolute
b= basic known conditions
c = calculated condition
r = reading
x = plane 1, 2, 3, or other
The conventional terms used to describe fan performance in the United States are defined blow.
Fan Air Density
Air density is the mass per unit volume of the air. The density of a perfect gas is a function of its molecular weight, temperature, and pressure as indicated by
where :
M =molecular weight, dimensionless
T =absolute temperature, °R (K)
b = barometric pressure, in Hg (Pa)
where the subscript x indicates the plane of the measurements. For dry air this reduces to
This expression will usually be accurate enough even when moist air is involved. Fan air density is the density of the air corresponding to the total pressure and total temperature at the fan inlet
Fan Capacity
Volume flow rate is usually determined from pressure measurements, e.g., a velocity-pressure traverse taken with a Pitot static tube or a pressure drop across a flowmeter. The average velocity pressure for a Pitot traverse is
where:
Pvx = velocity pressure at plane x, in wg (Pa)
n= number or polytropic exponent
where subscript x indicates the plane of the measurements, subscript r indicates a reading at one station, n is the number of stations, and ∑ is the summation sign. The corresponding capacity is:
where :
𝜌 = fan air density, lbm/ft³ (kg/m³)
Q′x = volumetric flow rate at plane x, ft³/min (m³/s)
A =area, ft² (m²)
For a flow meter
where
C=coefficient of discharge of meter,
Y=expansion factor for gas,
𝛥p= measured pressure drop,
F=velocity-of-approach factor for the meter installation.
Fan capacity is the volumetric flow rate at fan air density
where
Q′ =fan capacity, ft³/min (m³/s)
Fan Total Pressure
Fan total pressure is the difference between the total pressure at the fan outlet and the total pressure at the fan inlet
where
pt = fan total pressure, in wg (Pa)
When the fan draws directly from the atmosphere.
pt1 = 0
When the fan discharges directly to the atmosphere,
pt2 = pv2
pv= fan velocity pressure, in wg (Pa)
If either side of the fan is connected to duct work, etc., and the measuring plane is remote, the measured values should be corrected for the approximate pressure drop
Fan Velocity Pressure
Fan velocity pressure is the pressure corresponding to the average velocity at the fan outlet
pv = fan velocity pressure, in wg (Pa)
𝜌 = fan air density, lbm/ft³ (kg/m³)
A =area, ft² (m²)
Q′ =fan capacity, ft³/min (m³/s)
Fan Static Pressure
Fan static pressure is the difference between the fan total pressure and the fan velocity pressure. Therefore, fan static pressure is the difference between the static pressure at the fan outlet and the total pressure at the fan inlet
ps = fan static pressure, in wg (Pa)
pv = fan velocity pressure, in wg (Pa)
pt = fan total pressure, in wg (Pa)
Fan Speed
Fan speed is the rotative speed of the impeller.
Compressibility Factor The compressibility factor is the ratio of the fan total pressure p′t that would be developed with an incompressible fluid to the fan total pressure pt that is developed with a compressible fluid, all other conditions being equal:
Kp = compressibility factor, dimensionless
Compressibility factor can be determined from test measurements using
𝛾 = isentropic exponent, dimensionless
H = fan power input, hp (W)
z =factor used to determine Kp , dimensionless
x = factor used to determine Kp , dimensionles
Fan Power Output
Fan power output is the product of fan capacity and fan total pressure and compressibility factor
H0 = fan power output, hp (W)
Fan Power Input Fan power input is the power required to drive the fan and any elements in the drive train which are considered a part of the fan. Power input can be calculated from appropriate measurements for a dynamometer, torque meter, or calibrated motor.
Fan Total Efficiency
Fan total efficiency is the ratio of the fan power output to the fan power input
𝜼t = fan total efficiency, per unit
Fan Static Efficiency
Fan static efficiency is the fan total efficiency multiplied by the ratio of fan static pressure to fan total pressure
ps = fan static pressure, in wg (Pa)
pt = fan total pressure, in wg (Pa)
𝜼s = fan static efficiency, per unit
Fan Sound Power
Level Fan sound power level is 10 times the logarithm (base 10) of the ratio of the actual sound power in watts to 10⁻¹² watts,
Fan sound power level can be calculated from sound pressure-level measurements in a known acoustical environment. The standard laboratory method of testing is to use a calibrated sound source to calibrate a semireverberant room. In-duct test methods are being developed. The total sound power level of a fan is usually assumed to be 3 dB higher than either the inlet or outlet component. The casing component varies with construction but will usually range from 15 to 30 dB less than the total.
Head
The difference between head and pressure is important in fan engineering. Both are measures of the energy in the air. Head is energy per unit weight and can be expressed in ft . lb/ lb, which is often abbreviated to ft (of fluid flowing). Pressure is energy per unit volume and can be expressed in ft ? lb/ft³, which simplifies to lb/ft³ or force per unit area. The use of the inch water gage (in wg) is a convenience in fan engineering reflecting the usual methods of measurement. It sounds like a head measurement but is actually a pressure measurement corresponding to 5.192 lb/ft², the pressure exerted by a column of water 1 inch high. Pressures can be converted into heads and vice versa:
h = head, ft (m)
𝛒 = fan air density, lbm/ft³ (kg/m³)
Horsepower: a rate of doing work expressed in foot-pounds per minute.
HP = (RPM x torque) / 5252 lb-ft.
Fan Troubleshooting Guide
Low Capacity or Pressure
• Incorrect direction of rotation – Make sure the fan rotates in same direction as the arrows on the motor or belt drive assembly.
• Poor fan inlet conditions –There should be a straight, clear duct at the inlet.
• Improper wheel alignment.
Excessive Vibration and Noise
• Damaged or unbalanced wheel.
• Belts too loose; worn or oily belts.
• Speed too high.
• Incorrect direction of rotation. Make sure the fan rotates in same direction as the arrows on the motor or belt drive assembly.
• Bearings need lubrication or replacement.
• Fan surge.
Overheated Motor
• Motor improperly wired.
• Incorrect direction of rotation. Make sure the fan rotates in same direction as the arrows on the motor or belt drive assembly.
• Cooling air diverted or blocked.
• Improper inlet clearance.
• Incorrect fan RPM.
• Incorrect voltage.
Overheated Bearings
• Improper bearing lubrication.
• Excessive belt tension.
Fan Laws
The fan laws are based on the experimentally demonstrable fact that any two members of a homologous series of fans have performance curves which are homologous. At the same point of rating, i.e., at similarly situated points of operation on their characteristic curves, efficiencies
are equal and other variables are interrelated according to the fan laws.
If size and speed are considered independent variables and if compressibility effects are ignored, the fan laws can be written as follows:
The above laws are useful, but they are dangerous if misapplied. The calculated fan must have the same point of rating as the known fan.
When in doubt, it is best to reselect the fan rather than attempt to use the fan laws.
The fan designer utilizes the fan laws in various ways. Some of the more useful relationships in addition to those above derive from considering fan capacity and fan total pressure as the independent variables.
This leads to specific diameter, specific speed, and specific sound power level:
Ds , Ns , and Lws are the diameter, speed, and sound power level of a homologous fan which will deliver 1 ft³/min at 1 in wg at the same point of rating as Q and pt for D and N. Ds and Ns can be used to advantage in fan selection. They can also be used by a designer to determine how
well a line will fit in with other lines. Note the trends for each kind of fan. Incidentally, some fan engineers utilize different formulas for specific diameter and specific speed
where pte is the equivalent total pressure based on standard air. This makes Dse = Ds×1.911 and
Nse = Ns × 6.978. Specific sound power level is useful in predicting noise levels as well
as in comparing fan designs. There appears to be a lower limit of Lws in the vicinity of forty-five dB for the more efficient types ranging to 70 dB or more for cruder designs. Actual sound power levels can be figured from
Another useful parameter which derives from the fan laws is orifice ratio
This ratio can be plotted on a characteristic curve for a known fan. If theratio is determined for a calculated homologous fan, the point of rating can be established by inspection. Other ratios can be used in the same manner including pv /pt , pt / Q′2, Ds , and Ns .
Symbols
A = area, ft² (m²)
b =barometric pressure, in Hg (Pa)
D = diameter, ft (m)
Ds = specific diameter, ft (m)
H = fan power input, hp (W)
H0 = fan power output, hp (W)
h = head, ft (m)
Kp = compressibility factor, dimensionless
Lp = sound pressure level, dB
Lw = sound power level, dB
Lws = specific sound power level, dB
log = logarithm to base 10
M = molecular weight, dimensionless
N′= speed of rotation, r/min
Ns = specific speed, r/min
n = number or polytropic exponent
ps= fan static pressure, in wg (Pa)
pt = fan total pressure, in wg (Pa)
pv = fan velocity pressure, in wg (Pa)
psx = static pressure at plane x, in wg (Pa)
Ptx = total pressure at plane x, in wg (Pa)
Pvx = velocity pressure at plane x, in wg (Pa)
Q′= fan capacity, ft3/min (m³/s)
Q′x = volumetric flow rate at plane x, ft³/min (m³/s)
T = absolute temperature, °R (K)
W = power, W
x = factor used to determine Kp , dimensionless
z = factor used to determine Kp , dimensionless
𝛾 = isentropic exponent, dimensionless
𝜂s= fan static efficiency, per unit
𝜂t = fan total efficiency, per unit
𝜌 = fan air density, lbm/ft³ (kg/m³)
𝜌x =air density at plane x, lbm/ft³ (kg/m³)
A system characteristic
curve based on total pressure is plotted in Fig. characteristic based on static pressure is also shown. The latter recognizes the definition of fan static pressure so that the only difference is the velocity pressure corresponding to the fan outlet velocity.
This system could operate at any capacity provided a fan delivered the exact pressure to match the energy requirements shown on the system curve for that capacity.
 |
| Fan and system characteristics |
Labels: MECHANICAL ENGINEERING






















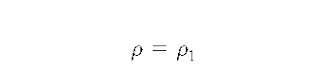



















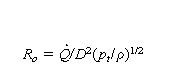



6 Comments:
Thank you for your wonderful information check_out most reputed
Axial flow Fan manufacturers Chennai
Thanks you for sharing this unique useful information content with us. Really awesome work. keep on blogging Centrifugal Fan manufacturers
This is the first time I am visiting your website. I would like to tell you that I am genuinely engaged by reading your blogs. Keep up the good work! centrifugal fan manufacturers
Excellent service and information. Great. Please continue
ok
Axial fans
Post a Comment
thanks for your visit
Subscribe to Post Comments [Atom]
<< Home