SIMPLE TRUSS CASE STUDY SIMPLE TRUSS CASE STUDY
the determination of the forces internal to a structure—that is, forces of action and reaction between the connected members. An engineering structure is any connected system of members built to support or transfer forces and to safely withstand the loads applied to it. To determine the forces internal
This analysis requires careful application of Newton’s third law, which states that each action is accompanied by an equal and opposite reaction .the internal forces acting in several types
of structures—namely, trusses, frames, and machines
The analysis of trusses, frames and machines, and beams under concentrated loads constitutes a straightforward application of the material
Characteristics of trusses
Thus, if we consistently draw the force arrows on the same side of the pin as the member, then tension (such as AB) will always be indicated by an arrow away from the pin, and compression (such as AF) will always be indicated by an arrow toward the pin.
Design of members
the lower horizontal member (the bottom chord) and the upper horizontal member (the top chord) carry tension and compression, fulfilling the same function as the flanges of an I-beam. Which chord carries tension and which carries compression depends on the overall direction of bending
Design of joint,s
SIMPLE TRUSS CASE STUDY
the determination of the forces internal to a structure—that is, forces of action and reaction between the connected members. An engineering structure is any connected system of members built to support or transfer forces and to safely withstand the loads applied to it. To determine the forces internal
This analysis requires careful application of Newton’s third law, which states that each action is accompanied by an equal and opposite reaction .the internal forces acting in several types
of structures—namely, trusses, frames, and machines
The analysis of trusses, frames and machines, and beams under concentrated loads constitutes a straightforward application of the material
Characteristics of trusses
Simple truss
framework composed of members joined at their ends to form a rigid structure is called a truss. Bridges, roof supports, derricks, and other such structures are common examples of trusses. Structural members commonly used are I-beams, channels, angles, bars, and special shapes which are fastened together at their ends by welding, riveted connections, or large bolts or pins. When the members of the truss lie essentially in a single plane, the truss is called a plane truss.
For bridges and similar structures, plane trusses are commonly utilized in pairs with one truss assembly placed on each side of the structure.
commonly used trusses
Commonly Used Bridge Trusses
Commonly Used Roof Trusses
The basic element of a plane truss is the triangle.Three bars joined by pins at their ends, Fig.1, constitute a rigid frame.The term rigid is used to mean noncollapsible and also to mean that deformation of the members due to induced internal strains is negligible.
On the other hand, four or more bars pin-jointed to form a polygon of as many sides constitute a nonrigid frame.
We can make the nonrigid frame in FIG 2 rigid, or stable, by adding a diagonal bar joining A and D or B and C and thereby forming two triangles.
The member may be in tension or compression .the tension T or compression C acting on the cut section is the same for all sections. figure 4
Truss Connections and Supports
Statics of trusses
In order for a truss with pin-connected members to be stable, it does not need to be entirely composed of triangles. In mathematical terms, we have the following necessary condition for stability of a simple truss:
framework composed of members joined at their ends to form a rigid structure is called a truss. Bridges, roof supports, derricks, and other such structures are common examples of trusses. Structural members commonly used are I-beams, channels, angles, bars, and special shapes which are fastened together at their ends by welding, riveted connections, or large bolts or pins. When the members of the truss lie essentially in a single plane, the truss is called a plane truss.
For bridges and similar structures, plane trusses are commonly utilized in pairs with one truss assembly placed on each side of the structure.
commonly used trusses
Commonly Used Bridge Trusses
Commonly Used Roof Trusses
The basic element of a plane truss is the triangle.Three bars joined by pins at their ends, Fig.1, constitute a rigid frame.The term rigid is used to mean noncollapsible and also to mean that deformation of the members due to induced internal strains is negligible.
 |
| FIG 1 |
 |
| FIG2 |
Structures built from a basic triangle in the manner described are known as simple trusses. When more members are present than are needed to prevent collapse, the truss is statically indeterminate. A statically indeterminate truss cannot be analyzed by the equations of equilibrium alone. Additional members or supports which are not necessary for maintaining the equilibrium configuration are called redundant.
To design a truss we must first determine the forces in the various members and then select appropriate sizes and structural shapes to with stand the forces. Several assumptions are made in the force analysis of simple trusses. First, we assume all members to be two-force members.
A two-force member is one in equilibrium under the action of two forces only
Each member of a truss is normally a straight link joining the two points of application of force. The two forces are applied at the ends of the member and are necessarily equal, opposite, and collinear for equilibrium.The member may be in tension or compression .the tension T or compression C acting on the cut section is the same for all sections. figure 4
 |
| FIG 4 |
When welded or riveted connections are used to join structural members, we may usually assume that the connection is a pin joint if the centerlines of the members are concurrent at the joint
For large trusses, a roller, rocker, or some kind of slip joint is used at one of the supports to provide for expansion and contraction due to temperature changes and for deformation from applied loads. Trusses and frames in which no such provision is made are statically indeterminate
In order for a truss with pin-connected members to be stable, it does not need to be entirely composed of triangles. In mathematical terms, we have the following necessary condition for stability of a simple truss:
m ≥ 2× j -r
where
m is the total number of truss members,
j is the total number of joints
r is the number of reactions (equal to 3 generally) in a 2-dimensional structure
When 
, the truss is said to be statically determinate, because the (m+3) internal member forces and support reactions can then be completely determined by 2j equilibrium equations, once we know the external loads and the geometry of the truss. Given a certain number of joints, this is the minimum number of members, in the sense that if any member is taken out (or fails), then the truss as a whole fails. While the relation is necessary, it is not sufficient for stability, which also depends on the truss geometry, support conditions and the load carrying capacity of the members.
, the truss is said to be statically determinate, because the (m+3) internal member forces and support reactions can then be completely determined by 2j equilibrium equations, once we know the external loads and the geometry of the truss. Given a certain number of joints, this is the minimum number of members, in the sense that if any member is taken out (or fails), then the truss as a whole fails. While the relation is necessary, it is not sufficient for stability, which also depends on the truss geometry, support conditions and the load carrying capacity of the members.
Two methods for the force analysis of simple trusses
Method of Joints
This method for finding the forces in the members of a truss consists of satisfying the conditions of equilibrium for the forces acting on the connecting pin of each joint. The method therefore deals with the equilibrium of concurrent forces, and only two independent equilibrium equations are involved.
We begin the analysis with any joint where at least one known load exists and where not more than two unknown forces are present.
The solution may be started with the pin at the left end. Its free-body diagram is shown
With the joints indicated by letters, we usually designate the force in each member by the two letters defining the ends of the member. The proper directions of the forces should be evident by inspection for this simple case
With the joints indicated by letters, we usually designate the force in each member by the two letters defining the ends of the member. The proper directions of the forces should be evident by inspection for this simple case
The free-body diagrams of portions of members AF and AB are also shown to clearly indicate the
mechanism of the action and reaction. The member AB actually makes contact on the left side of the pin, although the force AB is drawn from the right side and is shown acting away from the pin.
The magnitude of AF is obtained from the equation ΣFy = 0 and AB is then found from ΣFx = 0.
Method of Sections
This method of sections has the basic advantage that the force in almost any desired member may be found directly from an analysis of a section which has cut that member
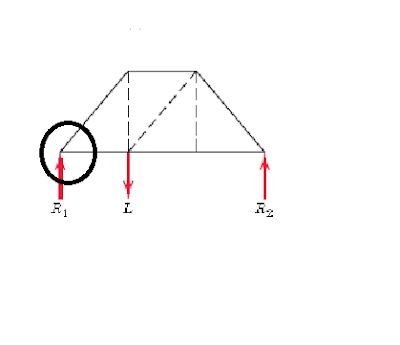
Let us determine the force in the member BE, for example. An imaginary section, indicated by the dashed line, is passed through the truss, cutting it into two parts,
This section has cut three members whose forces are initially unknown. In order for the portion of
the truss on each side of the section to remain in equilibrium, it is necessary to apply to each cut member the force which was exerted on it by the member cut away these forces, either tensile or compressive, will always be in the directions of the respective members.
We can usually draw the forces with their proper senses by a visual approximation of the equilibrium requirements.
Thus, in balancing the moments about point B for the left-hand section, the force EF is clearly
to the left, which makes it compressive, because it acts toward the cut section of member EF. The load L is greater than the reaction R1, so that the force BE must be up and to the right to supply the needed upward component for vertical equilibrium. Force BE is therefore tensile, since it acts away from the cut section
With the approximate magnitudes of R1 and L in mind we see that the balance of moments about point E requires that BC be to the right. A casual glance at the truss should lead to the same conclusion when it is realized that the lower horizontal member will stretch under the tension
caused by bending. The equation of moments about joint B eliminates three forces from the relation, and EF can be determined directly.
The force BE is calculated from the equilibrium equation for the y-direction. ΣFy = 0
Finally, we determine BC by balancing moments about point E. In this way each of the three unknowns has been determined independently of the other two
The right-hand section of the truss is in equilibrium under the action of R2 and the same three forces in the cut members applied in the directions opposite to those for the left section. The proper
sense for the horizontal forces can easily be seen from the balance of moments about points B and E.
The diagonal and vertical members form the truss web, and carry the shear stress
Once the force on each member is known, the next step is to determine the cross section of the individual truss members. For members under tension the cross-sectional area A can be found using
A = F × γ / σy
where
F is the force in the member,
γ is a safety factor (typically 1.5 but depending on building codes)
σy Is the yield tensile strength of the steel used.
The members under compression also have to be designed to be safe against buckling.
After determining the minimum cross section of the members, the last step in the design of a truss would be detailing of the bolted joints, e.g., involving shear stress of the bolt connections used in the joints. Based on the needs of the project, truss internal connections (joints) can be designed as rigid, semi rigid, or hinged. Rigid connections can allow transfer of bending moments leading to development of secondary bending moments in the members.
reference book engineering mechanics by Miriam
thanks for your visit