An introduction to Balancing
Unbalance is often defined as simply the unequal distribution of weight about a rotor’s centerline. Correction of this unequal distribution of weight about a rotor is called balancing. Balancing compensates for less-than-perfect manufacturing.
• Materials do not have uniform density
• Holes are not bored exactly parallel to the center
• Imperfections occur in machining round or symmetrical shapes
• Assembly errors. Unbalance can also occur during normal operation of machines. These causes are listed below:
• Uneven product deposition around a fan or pump impeller
• Damaged or missing blades or vanes
• Thermal distortion of the rotor due to temperature deviations in the process.
Balancing concepts
To improve an unbalanced rotor, it is necessary to determine
1- The heavy spot is the radial location where the excessive radial mass distribution exists
2-The high spot is the radial location where the shaft experiences maximum displacement during a rotation
There is a deterministic correlation between the heavy spot and the high spot. For rotors that run at speeds below the critical speed, the heavy spot and the high spot are in the same location.However on resonance that the heavy spot and the high spot can be as much as 180° apart after crossing the critical speed.
An unbalance condition involves phase measurements to locate the high spot, determining the relationship of the high spot to the heavy spot, and finding the magnitude of the unbalance by measuring the influence of correction weights.
In order to determine the unbalance, it is essential to learn how a perfectly balanced rotor responds to a mass that would tend to make it unbalanced. When an unbalance weight is added to a perfectly balanced rotor:
It vibrates at a frequency of 1× rpm.
• The measured phase will be steady, and under the strobe light a reference mark
will appear stationary (at any angle).
• If the weight of the unbalance is doubled, the vibration amplitude also doubles,
which implies the amplitude is proportional to the unbalance force.
• If the location of the unbalance weight is changed, the phase reading will
change If the unbalance weight is moved clockwise through a certain number of degrees, the phase reading or the reference mark under the strobe light will move by an equal number but in the opposite direction
Hence, the two important fundamentals of balancing are:
1. The amplitude of vibration is proportional to the severity of unbalance.
2. Reference marks shift in the direction opposite to the heavy spot. However, the angle of the shift of the heavy spot and the reference mark is the same.
The effect of a trial weight
To get the complete picture of the original unbalance A trial weight is a mass of known weight that is attached at a specific location with respect to the reference mark. When a trial weight is added, the original unbalance is disturbed. It may change for the better or worse, or not at all.
If the original unbalance does not change at all, it implies that the selection of the trial weight or its location on the rotor is inadequate. A heavier trial weight must be attached, or a different axial location must be used. As a rule of thumb, a trial weight should result in at least 30% change in vibration amplitude and phase.
Balancing methods
Single plane balancing – vector method
Single plane balancing is used for machines that operate below their critical speed and
have an L/D ratio lower than 0.5
where :
L, length of rotor, excluding support length;
D, diameter of the rotor
It is also recommended to avoid the use of this method for rotors operating at speeds greater than 1000 rpm
For cases where L/D ratio is greater than 0.5 but less than 2, this method should be applied for rotors that do not operate beyond 150 rpm. For L/D ratios greater than 2, the limit is 100 rpm. For this method of balancing, the following steps are taken:
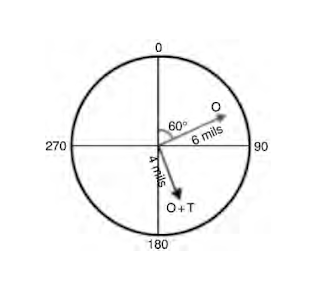
• During the first run, the original vibration and phase readings are recorded. For example, if the readings obtained are 6 mils (or mm, micron, etc.) at a phase angle of 60°, a polar plot can be constructed and a vector proportional to 6 mils is drawn at an angle of 60° from the 0° reference. This vector is called O (Figure 1).
• In the next step, a trial weight of 20 g is attached to the rotor at any location. During the subsequent measurement, we obtain the vibration and phase readings of 4 mils at 150°. It should be noted that the new values are due to the combined effect of the original unbalance and that of the trial weight. Let uscall this vector O + T (Figure 2).
With the above results we are in a position to determine the correction required to nullify the original unbalance of the rotor. The question is, if a vector T of 7.2 mils is generated by a trial weight of 20 g, what is the weight in grams that caused the original vector O?
= 16.7 g
Mathematically, we need to move the vector T in such a way to cancel the vector O. The movement should be equal in magnitude and opposite in direction. The angle between vector O and vector T is measured as 33.7°. Here, the vector T has to be moved clockwise to make it opposite to vector O. The new weight should be 16.7 g. It should be moved through 33.7° in the counterclockwise
direction (due to fundamental two of balancing) from its original point. Small errors due to angle measurement, positioning and other factors will result in a small residual unbalance. In case this residual unbalance is within the specified limits, the balancing is complete. Otherwise the above procedure must be repeated.
Two plane balancing – vector method
Single plane balancing has very limited application. Generally, all machines that have an L/D ratio of more than 0.5 should be balanced using the two-plane method. However, if a machine runs above it in critical speed, then the rule is N + 2 planes for balancing,
where N is number of critical speeds below the operating speed.
For example, a compressor operating above its first critical speed should be balanced using the three-plane balancing method.
Two-plane balancing is done in a manner similar to the single plane method. Two-plane balancing requires special attention due to the cross-effect or correction plane interference. Cross-effects occur when an indication of unbalance at one end of the rotor is actually caused by the unbalance at the opposite end. It is due to the cross-effect that unbalance indications at each end of the rotor do not represent the unbalance in the respective balancing planes.
Each indication is a result of the unbalance together with the cross-effect of the other plane. This phenomenon makes the two-plane method more complex than the single plane method. If it were not for the cross-effect, single plane balancing could have been done at each plane. Unfortunately, this does not work.
The two-plane vector method is described below. With the single-plane method, we had to make a minimum of two runs to obtain the required data. The two-plane method necessitates a minimum of three trial runs to acquire enough information for balancing correction. The procedure is briefly described as follows:
• The machine is started and the original amplitude and phase readings are recorded at each of the planes.
• A trial weight is selected and attached at the first plane. The weight and its phase angle should be recorded. The machine is started again and the amplitude and phase angle at each plane are measured and recorded.
The trial weight is then removed and installed on the other balancing plane. The machine is started once more and the amplitude and phase angle are recorded.
By using the results of the above three trial runs, it is possible to solve a 2 × 2 complex matrix of influence coefficients. Polar notation is useful in expressing complex numbers.
The matrix equation is: A ⋅ x = B,
where A is the 2 × 2 influence coefficient matrix;
x is the 2 × 1 correction mass vector;
B is the 2 × 1 vibration reading vector;
(A, x and B are all expressed in terms of complex numbers).
After this step, set vector B = 0 and solve vector x. The resulting vector x gives the correction mass and phase angle at each correction plane.
Balancing machines
There are four basic types of balancing machines:
1. Static balancing stands
2. Hard bearing machines
3. Soft bearing machines
4. High-speed machines.
Balancing limits
standard defines the balancing quality grade (G) as:
G = e ⋅ω
where e = eccentricity in mm;
ω = angular velocity of rotor in radians/second.
The standard specifies nine balancing grades that are applicable to various applications. The grades are stated as G 0.4, G 1, G 2.5, G 6.3, G 16, G 40, G 100, G 250 and G 630.The G 0.4 is the most strict grade and applies to rotors of gyroscopes, spindles and armatures of precision grinders, among others. The most lenient grade is G 630 and it is applicable to crankshaft of large and rigidly mounted diesel engines. The most commonly used grades for normal applications are G 2.5 and G 6.3. The former is applicable to most turbo machinery rotors and the latter is applicable to fans, pumps, motors and general machinery.
Angular velocity:
for more information see standard iso 1940
ISO 1940 is probably the most widely followed balancing standard
thanks for your visit